11609. Найти пары

Задано дерево с n вершинами. Вершина 1 считается корнем. Между любыми двумя вершинами существует единственный путь.

Обозначим d(i, j) как количество рёбер на пути от вершины i до вершины j.

Найдите количество таких пар вершин (i, j), для которых выполняется равенство:

d(i, j) = d(i, 1) – d(j, 1)

Вход. Первая строка содержит одно целое число n (1 ≤ n ≤ 10⁵) – количество вершин в дереве.

Каждая из следующих n – 1 строк содержит по два целых числа – описание рёбер дерева: пары вершин, соединённых ребром.

Выход. Выведите одно целое число – количество таких пар (i, j), для которых выполняется d(i, j) = d(i, 1) – d(j, 1).

Пример входа	Пример выхода
5 1 2 2 3 2 4 4 5	13

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

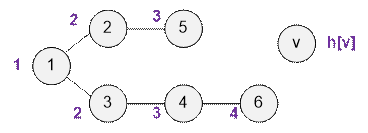
Условие d(i, j) = d(i, 1) – d(j, 1) выполняется для каждой пары вершин (i, j), у которой j является предком i при поиске в глубину из вершины 1. Рассмотрим пример:

· d(4, 1) = 2, d(4, 1) – d(1, 1) = 2 – 0 = 2;

· d(6, 3) = 2, d(6, 1) – d(3, 1) = 3 – 1 = 2;

· d(2, 2) = 0, d(2, 1) – d(2, 1) = 1 – 1 = 0;

· d(6, 1) = 3, d(6, 1) – d(1, 1) = 3 – 0 = 3;

Глубиной h[v] вершины v назовем количество вершин на пути от корня (вершины 1) до v. На рисунке глубина указана возле каждой вершины.

Зафиксируем вершину i и ответим на вопрос: сколько существует вершин j, для которых выполняется условие d(i, j) = d(i, 1) – d(j, 1).

Например, для i = 6 существуют 4 такие вершины: j = 1, 3, 4, 6. Заметим, что h[6] = 4. Таким образом, для фиксированной вершины i существует ровно h[i] подходящих вершин j.

Для решения задачи необходимо для каждой вершины v дерева вычислить её глубину h[v], а затем найти сумму всех значений глубин по дереву.

Пример

Рассмотрим граф из примера. Возле каждой вершины запишем ее глубину.

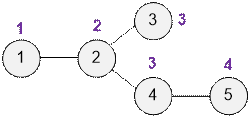
Сумма глубин всех вершин равна 1 + 2 + 3 + 3 + 4 = 13.

Реализация алгоритма

Объявим список смежности графа g. Глубину вершин храним в массиве h.

vector<vector<int> > g;

vector<int> h;

Функция dfs для каждой вершины v вычисляет ее глубину. Предком вершины v является вершина p.

int dfs(int v, int p)

{

for (int to : g[v])

Рассматриваем ребро (v, to). Если вершина to не является предком вершины v, вычисляем ее глубину и запускаем из нее поиск в глубину.

if (to != p)

{

h[to] = h[v] + 1;

dfs(to, v);

}

return h[v];

}

Основная часть программы. Читаем количество вершин дерева n.

scanf("%d", &n);

g.resize(n + 1);

Строим дерево.

for (i = 2; i <= n; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

g[b].push_back(a);

}

Глубину вершины 1 положим равной 1.

h.resize(n + 1);

h[1] = 1;

Запускаем поиск в глубину, начиная с вершины 1.

dfs(1, -1);

Вычисляем ответ – сумму глубин всех вершин.

res = 0;

for (i = 1; i <= n; i++)

res += h[i];

Выводим ответ.

printf("%lld\n", res);